Applications of a Queue in Daily life

Definition of Queue

A Queue is "an abstract data type in which elements are added to the rear and removed from the front; a 'first in, first out' (FIFO) structure."
(C++ Plus Data Structures, page 226)

The main difference between a queue and a stack is that elements in a queue are put on the bottom and taken off the top (remember, in a stack, elements put on the top and taken off the top). For an everyday queue example, consider a line of customers at a bank waiting to be served. Each new customer gets in line at the rear. When the teller is ready to help a new customer, the customer at the front of the line is served. This is a queue--the first customer in line is the first one served.

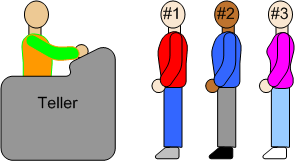
1.1 Applications of a Queue

In general, queues are often used as "waiting lines". Here are a few examples of where queues would be used:

In operating systems, for controlling access to shared system resources such as printers, files, communication lines, disks and tapes.A specific example of print queues follows:
- In the situation where there are multiple users or a networked computer system, you probably share a printer with other users. When you request to print a file, your request is added to the print queue. When your request reaches the front of the print queue, your file is printed. This ensures that only one person at a time has access to the printer and that this access is given on a first-come, first-served basis.
For simulation of real-world situations. For instance, a new bank may want to know how many tellers to install. The goal is to service each customer within a "reasonable" wait time, but not have too many tellers for the number of customers. To find out a good number of tellers, they can run a computer simulation of typical customer transactions using queues to represent the waiting customers.
When placed on hold for telephone operators. For example, when you phone the toll-free number for your bank, you may get a recording that says, "Thank you for calling A-1 Bank. Your call will be answered by the next available operator. Please wait." This is a queuing system.

1.2 Typical Operations of a Queue

	`clear()`	Removes all the elements from a queue
	`bool isEmpty`	Determines whether the queue is empty
	`bool isFull`	Determines whether the queue is full
	`enqueue(ItemType item)`	Adds an item to the rear of the queue
	`ItemType dequeue()`	Removes front item from the queue and returns it
	`showStructure()`	Outputs the elements of a queue

2. Application: Using Queues for Simulations

The following section outlines an algorithm for simulating the flow of customers through a check-out line. Later, in the lab exercise, you will be given a chance to add code to complete this program.

Waiting is the critical element of queues. The objective of a queuing system is to utilize the servers (the tellers, CPU, operators, and so on) as fully as possible, while keeping the wait time within a reasonable limit.

So, in real life, how does a company determine the optimal compromise between the number of servers and the wait time? One way is through experience. The company tries out different numbers of servers and sees how things work out. There are two problems with this approach: 1) it takes too long, and 2) it is too expensive. A better approach is to use a computer simulation of the tellers, customers, and wait time. This approach uses queues.

2.1 The Algorithm

We can use a queue to simulate the flow of customers through a check-out line in a store. In this simulation we will have the following details:

one check-out line
the expected service time for each customer is one minute (However, they may have to wait in line before being serviced)
between zero and two customers join the line every minute

In addition, the algorithm will keep track of the following:

the total number of customers served
the combined total wait time of all customers
the maximum length of time any of these customers spent waiting in line

2.2 Operations on the Queue for the Check-out Line Simulation

Given a time of 5 minutes, the following demonstrates the operations on the queue:

minute	queue isempty?	k	queue operations
0	yes		no dequeue (empty queue)
0	yes	1	enqueue(0)
1	no
			dequeue
		2	enqueue(1)
		2	enqueue(1)
2	no
			dequeue
		2	enqueue(2)
		2	enqueue(2)
3	no
			dequeue
		1	enqueue(3)
4	no
			dequeue
		0	no enqueue (k=0)